The Law of the Lever
weight and balance 문제는 지렛대의 법칙에 기초한다. 지렛대의 법칙은 다음과 같다: 지렛대의 중심점으로부터 한쪽에 위치한 무게에 arm을 곱한 것이 반대쪽에 있는 무게에 arm을 곱한 것과 같다면 지렛대가 균형을 이룬다. 즉, 지렛대의 중심점에 대한 모멘트들의 합이 0이면 지렛대가 균형을 이룬다. 이는 양(+)의 모멘트(지렛대를 시계방향으로 회전시키려는 힘)가 음(-)의 모멘트(지렛대를 반시계방향으로 회전시키려는 힘)와 같은 상태이다. 항공기에서는 이러한 균형점을 CG라 부른다.
weight and balance를 이해하는 가장 쉬운 방법들 중 하나는 여러 위치에 무게가 배치된 지렛대를 고려하는 것이다. 무게를 지렛대의 중심점으로부터 더 가깝게(혹은 더 멀게) 이동시키거나 무게를 증가(혹은 감소)시킴으로써 지렛대의 CG를 바꿀 수 있다. 지렛대의 CG는 다음 네 단계를 통해 결정될 수 있다:
1. 각 무게의 arm(인치 단위)을 datum으로부터 측정한다.
2. 각 arm을 그 무게(파운드 단위)와 곱해서 각 무게의 모멘트(파운드-인치 단위)를 결정한다.
3. 총 무게와 총 모멘트를 결정한다. (단, 지렛대의 무게는 무시한다.)
4. 총 모멘트를 총 무게로 나눠서 중심점을 결정한다.
그림 2-1의 지렛대를 통해 이를 고려해보자. A(100 파운드)는 지렛대 중심점(이 예시에서는 지렛대 중심점이 곧 datum임)으로부터 50인치 왼쪽에 위치한다. 이는 –5,000 lb-in(100 x –50)의 모멘트를 갖는다. B(200 파운드)는 지렛대 중심점으로부터 25인치 오른쪽에 위치한다. 이는 +5,000 lb-in(200 x +25)의 모멘트를 갖는다. 모멘트들의 합은 0(-5,000 + 5,000)이며 지렛대는 균형을 이룬다. [그림 2-2] 시계방향으로 회전하려는 힘은 시계반대방향으로 회전하려는 힘과 동일한 크기를 갖는다. 무게가 이동하거나 바뀌면 CG가 변화하고 지렛대가 불균형해진다.

그림 2-3에서 datum은 지렛대의 왼쪽 바깥에 위치한다. 그림 2-3의 정보를 통해 차트를 작성해서 균형점을 결정한다. [그림 2-4]

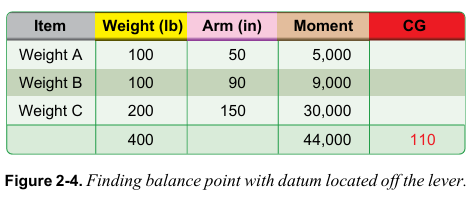
A의 무게는 100 파운드이며 이는 datum으로부터 50인치에 위치한다. B의 무게는 100 파운드이며 이는 datum으로부터 90인치에 위치한다. C의 무게는 200 파운드이며 이는 datum으로부터 150인치에 위치한다. 총 무게는 400 파운드이고 총 모멘트는 44,000 lb-in이다.
총 모멘트를 총 무게로 나눠서 균형점을 결정한다. 균형점이 곧 CG이며 이는 수학적으로 다음과 같이 쓸 수 있다:
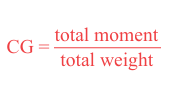
이 균형점이 올바르다는 것을 증명하기 위해 datum을 원래의 위치에서 오른쪽으로 110인치 이동한다. 그리고 새로운 datum에서 각 무게의 arm을 결정한다. [그림 2-5] 그런 다음 차트를 작성한다. [그림 2-6] 균형점이 올바르다면 모멘트들의 합이 0일 것이다.
A의 새로운 arm은 60인치이지만 무게가 datum으로부터 왼쪽에 있으므로 음수이다(-60). B의 새로운 arm은 20인치이지만 이 무게 또한 datum으로부터 왼쪽에 있으므로 음수이다(-20). C의 새로운 arm은 40인치이며 이는 datum의 오른쪽에 있으므로 양수이다(+40).
모멘트들의 합이 0일 때 지렛대는 균형을 이룬다. 무게의 arm을 결정할 때 사용되는 datum의 위치는 중요하지 않다. datum은 어디에든 있을 수 있다. 허나 모든 측정은 동일한 datum 위치로부터 수행되어야 한다.
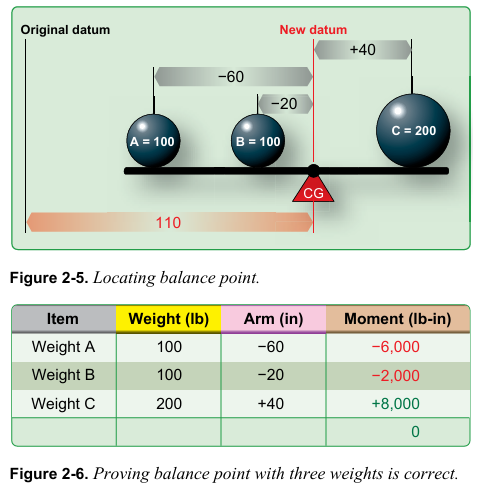
균형점을 찾는 절차는 datum이 어디에 위치하든 동일하다. 그림 2-7에서 datum은 C에 위치한다. A는 datum으로부터 –100인치의 arm을 가진다. B는 datum으로부터 –60인치의 arm을 가진다. 새로운 균형점을 결정하기 위해 그림 2-8의 표가 사용된다.
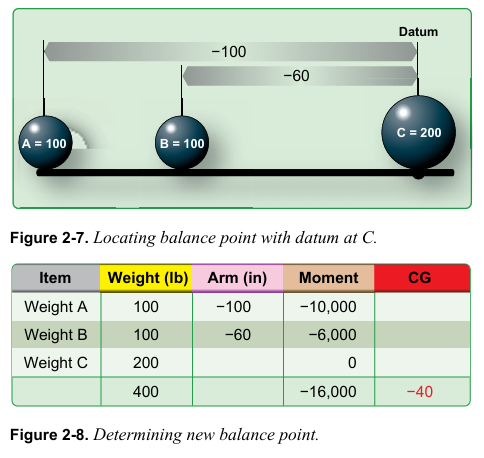
이것이 정확한 균형점인지 확인하기 위해 datum을 원래의 위치에서 40인치 왼쪽으로 움직인다. 그리고 새로운 datum으로부터 각 무게의 arm을 측정한다. [그림 2-9]
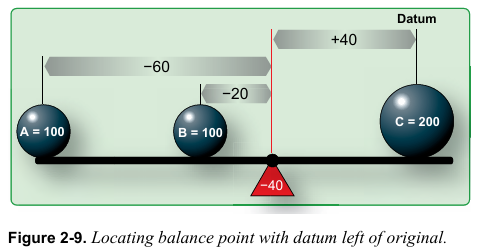
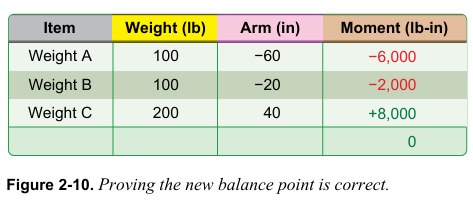
A의 새로운 arm은 –60이다. B의 새로운 arm은 –20이다. C의 새로운 arm은 +40이다. 모멘트들의 합이 0일 경우 지렛대가 균형을 이루며 균형점이 정확하다. [그림 2-10]
'Weight and Balance(2016) > 2: Weight and Balance Theory' 카테고리의 다른 글
| (1) Introduction (0) | 2023.06.24 |
|---|---|
| (2) Weight and Balance Theory (0) | 2023.06.24 |
| (4) Shifting the Balance Point or CG (0) | 2023.06.24 |
| (5) Mean Aerodynamic Chord (0) | 2023.06.24 |
| (6) FAA-Furnished Weight and Balance Information (0) | 2023.06.24 |