(4) Shifting the Balance Point or CG

Shifting the Balance Point or CG

 

한 가지 일반적인 weight and balance 문제는 CG를 원하는 위치로 이동하기 위해 무게를 한 지점에서 다른 지점으로 이동하는 것이다. 이는 세 개의 무게를 가진 지렛대를 통해 문제를 해결함으로써 증명될 수 있다.

 

Solution by Chart

 

그림 2-11에서 균형점은 A로부터 72인치 지점에 잡힌다.

 

B를 이동하여 지렛대의 균형점을 50인치 지점으로 만들기 위해선 원하는 균형점에 대해 세 가지 무게의 총 모멘트가 0을 만들어내는 B의 arm을 결정한다. 새로운 균형점에 대한 A와 C의 모멘트 합은 5,000 lb-in이다. 따라서 지렛대가 균형을 이루려면 B의 모멘트가 –5,000 lb-in 이어야 한다. [그림 2-12]

 

B의 모멘트(-5,000 lb-in)을 무게(200 파운드)로 나누어 arm(-25 인치)을 결정한다. 지렛대의 중심으로부터 왼쪽 25인치 지점에 B를 배치시킴으로써 지렛대의 균형을 맞춘다. [그림 2-13]

※ 그림 2-13의 C는 200 파운드인데 그림이 잘못됨.

 

그림 2-14는 무게 이동을 통한 모멘트의 합이 0이므로 지렛대가 균형을 이룰 수 있음을 나타낸다.

 

Basic Weight and Balance Equation

 

다음 공식을 통해 특정 CG 변화를 위한 distance weight is shifted를 결정할 수 있다. 특정 CG 변화를 위한 weight shifted, 특정 무게 변화에 대한 △CG, 혹은 특정 CG 변화를 위한 특정 무게의 이동을 허용하는 총 무게를 찾도록 방정식을 재 정렬할 수도 있다.

 

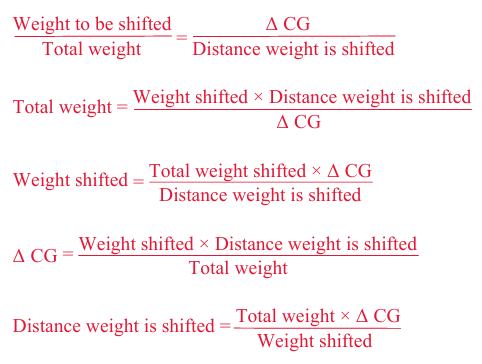
Solution by Formula

 

그림 2-11의 문제는 기본 방정식을 변형하여 해결될 수 있다. 먼저 B의 distance weight is shifted를 구하기 위해 공식을 재 정렬한다:

 

그림 2-11의 지렛대 CG는 datum으로부터 72인치 떨어져 있었다. 이 CG는 B의 이동을 통해 지렛대의 중앙으로 이동할 수 있다. [그림 2-13] B(200 파운드)가 왼쪽으로 55인치 이동하면 CG가 +72 인치에서 +50 인치(22인치 거리)로 이동한다.

 

distance weight is shifted를 알고 있는 경우 CG를 이동하기 위한 weight shifted는 기본 방정식의 다른 배열을 통해 결정될 수 있다. CG를 station +72에서 +50으로 이동하기 위해 station +80에서 +25로 이동해야 하는 무게를 결정하기 위해선 다음 공식을 사용한다.

 

B(200 파운드)가 station +80에서 +25로 이동하면 CG가 station +72에서 +50으로 이동한다.

 

기본 방정식의 세 번째 배열은 특정한 무게가 특정한 거리를 이동하였을 때 CG가 이동하는 거리를 결정하는데 사용된다. 다음 공식은 B(200 파운드)가 +80에서 +25로 이동할 때 CG가 이동하는 거리를 결정하는데 사용된다.

 

B를 +80에서 +25로 이동하면 CG가 원래의 위치(+72)에서 새로운 위치(+50)로 22인치 이동한다. [그림 2-13]

 

계산을 완료하기 위해 원래의 공식으로 돌아가 적절한 값들을 입력한다.

 

방정식이 일치한다.