Load Factors
최대 하중 계수는 양력과 무게 사이의 비율을 의미한다. 하중 계수는 G(중력가속도. 정지 상태의 물체에 중력이 가하는 힘의 단위)로 측정되며 이는 물체가 가속될 때 받는 힘을 나타낸다. 항공기를 직진 비행 상태로부터 벗어나게 만드는 모든 힘은 항공기 구조에 응력을 발생시킨다. 이러한 힘의 양이 하중 계수이다. 조종사는 항공기에 작용하는 힘, 이러한 힘의 유리한 용도, 그리고 비행중인 항공기의 운영 한계를 확실하게 이해해야 한다.
예를 들어 3의 하중 계수는 항공기 구조에 가해지는 총 하중이 3배임을 의미한다. 하중 계수는 G로 표현된다. 따라서 3의 하중 계수는 3G라 말할 수 있다.
항공기 급강하 도중 기수를 당겨서 3G가 가해지면 조종사는 본인 무게의 3배에 해당하는 힘으로 좌석에 눌릴 것이다. 현대의 항공기는 옛날 항공기보다 훨씬 빠른 속도로 운항하기 때문에 높은 하중 계수가 발생할 가능성이 더 높다. 따라서 이러한 영향이 모든 항공기의 구조 설계에서 주요 고려 사항이 되었다.
항공기 구조 설계가 특정한 양의 과부하만을 견딜 수 있도록 설계되므로 조종사는 하중 계수에 대한 지식을 알아야 한다. 하중 계수는 다음 두 가지 이유 때문에 중요하다:
1. 항공기 구조에 위험한 과부하를 가할 수 있다.
2. 하중 계수가 증가하면 실속 속도가 증가한다. 이로 인해 안전해 보이는 비행 속도에서도 실속이 발생할 수 있다.
Load Factors in Aircraft Design
“항공기의 강도는 어느 정도여야 하는가?”라는 질문에 답하자면 항공기가 사용되는 용도에 따라 달라진다. 이는 어려운 문제이다. 왜냐하면 효율적으로 설계하기엔 maximum possible loads가 너무 높기 때문이다. 어떠한 조종사도 hard landing을 수행할 수 있으며 이는 비정상적인 하중으로 이어질 것이다. 허나 빠르게 이륙하고 천천히 착륙하며 중요한 유상하중을 운반하는 항공기를 제작한다면 이러한 비정상적인 하중이 어느 정도 해소되어야 한다.
항공기 설계 시 하중 계수에 대한 문제는 정상 운영 도중 예상될 수 있는 가장 높은 하중 계수를 어떻게 결정할 것인가로 귀결된다. 이러한 하중 계수를 “limit load factors(한계 하중 계수)”라 부른다. 안전상의 이유를 위해 항공기는 이러한 하중 계수를 구조적 손상 없이 견딜 수 있도록 설계되어야 한다. CFR은 다음과 같이 명시한다: 항공기 구조물은 이러한 limit load factors의 1.5배를 구조적 파괴 없이 견딜 수 있어야 한다(단, 이러한 하중으로 인해 항공기의 일부가 뒤틀리거나 일부 구조적 손상이 발생하는 것은 허용한다).
이러한 1.5배의 load limit factor를 “factor of safety”라 부른다. 이는 정상 운영 도중 발생하리라 예상되는 하중보다 어느 정도 높은 하중을 대비할 수 있게 해준다. 이러한 예비 강도는 조종사가 의도적으로 사용할 수 있는 것이 아니다. 이는 예상치 못한 상황이 발생하였을 때 조종사를 보호하기 위한 것이다.
위의 고려 사항은 돌풍, 기동, 혹은 착륙으로 인한 모든 하중 조건에 적용된다. 현재 시행중인 gust load factor 조건은 수년 동안 존재해온 조건과 거의 동일하다. 이는 수십만 시간의 운항을 통해 안전에 적합하다는 것이 증명되었다. 조종사가 gust load factors를 제어할 수는 없으므로(단, 항공기 속도를 줄이는 것은 제외) gust load factor 조건들은 대부분의 범용 항공 항공기에 대해 실질적으로 동일하다. 보통 gust load factors는 곡예비행을 목적으로 하지 않는 항공기의 설계 조건을 규제한다.
maneuvering load factors가 있는 항공기 설계에서는 완전히 다른 상황이 존재한다. 이 문제는 다음과 관련하여 별도로 논의되어야 한다: (1) category system(즉, normal, utility, acrobatic)에 따라 설계된 항공기 (2) category를 제공하지 않는 조건에 따라 설계된 구형 항공기.
category system에 따라 설계된 항공기는 조종실의 placard를 통해 쉽게 식별될 수 있다. placard는 항공기에 대해 증명된 category를 명시한다. 특정 category에 대한 maximum safe load factors(limit load factors)는 다음과 같다:

※ 총 무게가 4,000파운드를 초과하는 normal category 항공기의 경우 limit load factor가 감소한다.
기동의 난이도가 높아질수록 하중 계수가 상향 조정된다. category system은 항공기의 활용도를 극대화하기 위한 것이다. normal operation만을 목적으로 하는 항공기에 필요한 하중 계수는 훈련이나 곡예비행에 필요한 하중 계수보다 작다.
category placard가 없는 항공기는 초기 설계 조건에 따라 제작된 항공기로 이는 조종사에게 특별한 운영 제한을 가하지 않는다. 약 4,000파운드 미만의 항공기 무게에 필요한 강도는 현재의 utility category aircraft와 거의 유사하며 동일한 유형의 운영이 허용된다. 항공기 무게가 4,000파운드를 초과하면 하중 계수가 무게에 따라 감소한다. 이러한 항공기는 normal category aircraft로 간주되어야 하며 이에 따라 운영되어야 한다.
Load Factors in Steep Turns
고도를 유지하면서 선회를 수행할 때 하중 계수는 두 가지 힘에 의해 발생한다: 원심력과 무게. [그림 5-52] 특정 bank angle에서 선회율은 대기속도에 따라 달라진다(대기속도가 높을수록 선회율은 느려지고 대기속도가 낮을수록 선회율은 빨라짐). 이는 추가적인 원심력을 보상하여 하중 계수가 동일하게 유지되도록 만든다(즉, 선회 시의 하중계수는 비행속도와 관계가 없다).
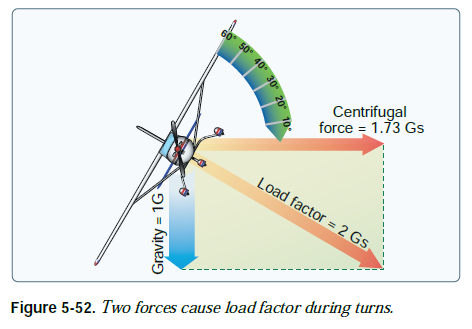
그림 5-53은 선회에 대한 중요한 사실을 보여준다. 바로 bank가 45도에 도달한 후에 하중 계수가 놀라운 속도로 증가한다는 것이다. 60도 bank에서 수평 선회 중인 항공기의 하중 계수는 2G이다. 80도 bank의 하중 계수는 5.76G이다. 고도를 유지하고자 한다면 날개가 이러한 하중 계수와 동일한 양력을 생성해야 한다.

90도 bank에 근접함에 따라 그래프가 얼마나 빠르게 상승하는지 주목한다. 90도 bank로 일정한 고도를 선회하는 것은 수학적으로 불가능하다. 고도를 유지지 않는 경우에는 90도 bank 선회를 수행할 수 있다. 90도 bank에서 slipping turn을 유지할 수 있는 항공기는 straight knife-edged flight를 수행할 수 있다. 80도가 약간 넘는 bank에서는 곡예비행기의 limit load factor인 6G가 초과된다.
일반적인 범용 항공 항공기가 고도를 유지하면서 선회를 할 때 사용하는 대략적인 최대 bank는 60도이다. 60도의 bank, 그리고 60도 bank에 필요한 출력은 범용 항공 항공기를 한계에 도달하게 만든다. bank가 10도 더 가해지면 하중 계수가 약 1G 증가한다. 이는 해당 항공기에 설정된 항복점(yield point)에 근접하게 만든다. [그림 5-54]


모든 항공기는 어느 비행 속도에서도 실속에 빠질 수 있다. 충분히 높은 받음각이 가해지면 에어포일 위의 원활한 공기 흐름이 분리되며 비행 특성의 급격한 변화와 급격한 양력 손실이 발생한다. 이는 곧 실속으로 이어진다.
항공기의 실속 속도는 하중 계수의 제곱근에 비례하여 증가한다. 즉, 정상적인 비가속 실속 속도가 50노트인 항공기에 4G의 하중 계수가 발생하면 항공기가 100노트에서 실속에 빠질 수 있다. 만약 이 항공기가 9G의 하중 계수를 견딜 수 있다면 항공기가 150노트에서 실속에 빠질 수 있다. 조종사는 다음 사항을 알고 있어야 한다:
∙ 하중 계수가 증가하면 의도치 않게 실속에 빠질 수 있다(예를 들어 steep turn이나 sprial 도중).
∙ design maneuvering speed를 초과한 속도에서 의도적으로 항공기를 실속시킬 경우 엄청난 하중 계수가 부과된다.
72도의 steep turn 도중 항공기에 3G의 하중 계수가 가해져 실속 속도가 크게 증가한다. [그림 5-53과 54] 정상적인 비가속 실속 속도가 45노트인 항공기로 이 선회를 수행하는 경우에는 대기속도를 75노트 이상 유지함으로써 실속을 방지해야 한다. 빠르게 기수를 당기거나 1G를 초과하는 기동을 수행할 때에도 이와 유사한 효과가 발생한다.
실속 속도가 두 배가 되면 하중 계수는 제곱이 된다. 따라서 상대적으로 높은 대기 속도에서 항공기가 실속에 빠지면 구조물에 엄청난 하중이 가해질 수 있다.
비행기가 안전하게 실속에 빠질 수 있는 최대 속도를 “design maneuvering speed”(VA)라 부른다. 이 속도 이하에서 조종사는 비행기 손상의 위험 없이 하나의 비행기 축(pitch, roll, 혹은 yaw)에 대해 하나의 조종간 입력을 한 번 full deflection으로 움직일 수 있다(단, 이는 smooth air를 조건으로 함). VA는 모든 비행기의 AFM/POH에 입력되어야 한다. 구형 범용 항공 비행기의 경우 이러한 속도는 정상 실속 속도의 약 1.7배이다. 따라서 60노트에서 실속에 빠지는 구형 비행기가 102노트(60노트 x 1.7 = 102)를 초과하는 속도에서 실속에 빠져선 안 된다. 실속 속도가 60노트인 비행기가 102노트에서 실속에 빠질 경우 2.89G(1.7 x 1.7 = 2.89)의 하중 계수를 겪는다. (해당 값은 참고용 수치이므로 제조업체가 제공하는 특정 항공기의 운영 한계[operating limitations]를 통해 design maneuvering speed를 결정해야 한다.) 설령 design maneuvering speed 이하로 비행하여도 하나의 축에 여러 번의 full control inputs를 가하거나, 혹은 두 개 이상의 축에 full control inputs를 가하면 구조적 보호가 제공되지 않는다.
조종간 시스템은 항공기마다 다르다. 따라서 조종간에 가해지는 압력을 하중 계수의 지표로 받아들일 수 없다. 대부분의 경우 하중 계수는 조종사가 느끼는 착석 압력(seat pressure)을 통해 판단될 수 있다. 하중 계수는 또한 “가속도계(accelerometer)”라 불리는 계기로도 측정될 수 있다. 그러나 해당 계기는 범용 항공 훈련용 항공기에서는 일반적이지 않다. 신체에 가해지는 영향을 통해 하중 계수를 판단하는 능력을 개발시키는 것은 중요하다. 이러한 원리에 대한 지식은 하중 계수를 추정하는 능력을 개발하는데 필수적이다.
가지각색의 bank angle로부터 발생하는 하중 계수를 알면 두 가지 유형의 심각한 사고를 예방하는데 도움이 된다:
1. steep turns나 과도한 기동으로 인한 실속.
2. 곡예비행이나 그 외 맹렬한 기동 도중 조종제어 상실(loss of control)로 인한 구조적 파괴.
Load Factors and Flight Maneuvers
하중 계수는 모든 비행 기동에 적용된다(단, 항상 1G의 하중 계수가 존재하는 비가속 직진 비행은 제외). 여기서 고려하는 특정 기동들은 상대적으로 높은 하중 계수를 수반한다. pitch, roll, 혹은 yaw를 full로 적용하는 것은 maneuvering speed 이하로 제한되어야 한다. 갑작스럽고 큰 조종간 입력 변화는 VA 이하에서도 구조적 파괴를 초래할 수 있으므로 이를 피한다(특히 pitch, roll, 혹은 yaw의 큰 변화가 함께 사용되는 경우. 예를 들어 큰 sideslip 각도).
Turns
하중 계수의 증가는 모든 선회의 특징이다. bank가 약 45도 이상으로 증가하면 하중 계수는 비행 성능과 날개 구조 부하에 중대한 영향을 미친다.
일반적인 소형 비행기의 limit load factors는 약 70 ~ 75도의 bank에서 도달한다. 실속 속도는 대략 63도의 bank에서 절반이 증가한다.
Stalls
직진수평비행으로부터 진입되는 실속, 혹은 비가속 직진 상승으로부터 진입되는 실속은 1G를 초과하는 추가 하중 계수를 생성하지 않는다. 그러나 실속이 발생하면 이 하중 계수가 0으로 감소하여 무게가 사라진 것처럼 느낄 수 있다. 이때 조종사는 “우주에서 자유롭게 떠다니는” 느낌을 경험한다. 만약 조종사가 elevator control을 급하게 밀어 회복을 수행하면 음(-)의 하중 계수가 발생할 수 있다.
실속 회복 후에 기수를 당길 때 종종 상당한 하중 계수가 발생한다. 이는 급강하(그리고 결과적으로 높은 대기속도) 도중에, 그리고 급격한 pull up 도중에 더욱 증가할 수 있다. 둘 중 하나는 보통 다른 하나로 이어져서 결국 하중 계수를 증가시킨다. 급강하 도중 급격하게 기수를 당기면 항공기 구조에 치명적인 부하를 가할 수 있다. 또한 받음각을 실속 받음각까지 증가시켜서 secondary stall이 발생할 수도 있다.
(ATP: 비행기가 부양한 후에 갑자기 기수를 당기거나 급선회를 수행하면 실속, 스핀, 혹은 상승률 감소로 이어질 수 있다.)
대기속도가 실속 속도 이상이 되었을 때 점진적으로 기수를 당기되 cruising airspeed나 design maneuvering airspeed 미만의 속도에서 실속이 회복되면 2G나 2.5G를 초과하지 않을 수 있다. 더 높은 하중 계수가 발생해서는 안 된다(단, 수직 자세에 가까운 항공기 상태로부터 회복이 수행되는 경우, 혹은 극도로 낮은 고도에서 회복이 수행되는 경우 제외).
Spins
스핀은 축을 중심으로 회전하는 것 이외의 다른 요소에서 실속과 다르지 않다. 때문에 실속 회복 도중 적용되는 하중 계수 고려 사항들이 스핀 회복 도중에도 적용된다. 스핀 회복은 보통 실속 회복보다 훨씬 낮은 기수에서 수행된다. 때문에 더 높은 대기속도와 이에 따른 더 높은 하중 계수가 예상된다. 올바른 스핀 회복 도중 발생하는 하중 계수는 보통 약 2.5G이다.
스핀 도중 발생하는 하중 계수는 항공기의 스핀 특성에 따라 다르다. 허나 이는 일반적으로 1G보다 약간 높다. 여기에는 두 가지 이유가 있다:
1. 스핀 도중 대기속도는 매우 낮다(보통 비가속 실속 속도로부터 2노트 이내).
2. 스핀 도중 항공기는 선회를 수행한다기 보다는 축을 중심으로 회전한다.
High Speed Stalls
소형 비행기는 high speed stalls 도중 발생하는 하중 계수가 반복적으로 적용되는 것을 견딜 수 있도록 제작되지 않는다. 이러한 기동에 필요한 하중 계수는 날개와 꼬리 구조에 응력을 발생시킨다. 이는 대부분의 소형 비행기에 안전 여유를 남기지 않는다.
이 실속을 정상 실속 속도보다 높은 대기속도에서 발생시킬 수 있는 유일한 방법은 추가 하중 계수를 부과하는 것이다. 이는 elevator control을 강하게 잡아당김으로서 이루어질 수 있다. 예를 들어 실속속도의 1.7배 속도는(실속 속도가 60노트인 소형 비행기의 경우 약 102노트) 3G의 하중 계수를 생성한다. 대기속도가 증가함에 따라 하중 계수도 빠르게 증가한다. 동일한 항공기가 112노트에서 high-speed stall에 빠지면 4G의 하중 계수가 생성된다.
Chandelles and Lazy Eights
chandelle은 직진수평비행에서 시작되는 최대 성능 상승 선회로 180도 선회가 완료되면 wing-level, nose-high attitude, 그리고 minimum controllable airspeed가 완성된다. 이 기동 도중 항공기는 가파른 상승 선회를 수행하며 상승하는 동안 거의 실속에 가까워진다. lazy eight는 항공기의 세로축이 “∞” 모양의 비행 패턴을 그리도록 만들어진 방법에서 그 이름이 유래되었다. 이러한 기동들의 하중 계수에 대해 명확하게 말하기는 어렵다. 왜냐하면 둘 다 매끄럽고 얕은 dive/pull-up을 포함하기 때문이다. 기동 도중 발생하는 하중 계수는 하강 속도, 그리고 pull-up 속도에 따라 달라진다.
보통 기동이 잘 수행될수록 하중 계수가 덜 극단적으로 발생한다. pull-up으로 인해 2G 이상의 하중 계수가 발생하면 고도가 크게 상승하지 않는다(출력이 낮은 항공기의 경우에는 고도가 떨어질 수도 있다).
최대한 매끄러운 pull-up이 가해지면 chandelle 도중 적당한 하중 계수와 함께 최대 고도 상승이 발생한다. 매끄러운 pull-up은 chandelle과 lazy eight의 전반적인 결과도 향상시킨다. 이러한 기동들을 위한 권장 진입 속도는 보통 제조업체의 design maneuvering speed 근처에 있다. 이를 통해 load limits를 초과하지 않고도 하중 계수를 최대로 증가시킬 수 있다.
Rough Air
항공기는 상당한 강도의 돌풍에 의해 부과되는 하중을 견딜 수 있도록 설계되었다. gust load factor는 비행 속도에 비례하여 증가하며 설계 목적을 위해 사용되는 강도는 보통 최대 비행 속도에 상응한다. 심한 rough air에서는(예를 들어 뇌우나 전선에서는) design maneuvering speed로 감속하는 것이 현명하다.
각 항공기는 구조적 손상 없이 항공기에 가해질 수 있는 특정 G loading을 갖는다. 항공기 설계에 고려되는 두 가지 유형의 하중 계수가 있다: limit load(한계 하중)와 ultimate load(종극 하중). limit load는 항공기 구조가 원래의 형태로 돌아가지 않는 굽힘을 일으킨다. ultimate load는 limit load를 초과하여 항공기에 가해지는 하중 계수로 이 지점에서 항공기 소재는 구조적 파괴를 경험한다. limit load보다 낮은 하중 계수는 항공기 구조를 손상시키지 않는다.
maneuvering speed 미만의 속도는 limit load가 초과되는 하중 계수가 발생하기 전에 항공기를 실속에 빠지게 만든다.
대부분의 AFM/POH는 turbulent air 통과 정보를 포함한다. 이는 광범위한 속도 및 고도를 비행할 수 있는 항공기를 안전하게 운항하는데 도움을 제공한다. “never-exceed” placard는 오직 smooth air에 대해 결정된 것임을 기억해야 한다. maneuvering speed를 초과하는 고속 하강이나 곡예비행을 rough air나 turbulent air에서 수행해서는 안 된다.
Vg Diagram
항공기의 운영 강도가 그래프에 표시된다. [그림 5-55] 그래프의 수직 눈금은 하중 계수를 기초로 한다. 이 도표를 Vg diagram(Vn diagram이라고도 불림)이라 부른다. 각 항공기는 특정 무게 및 고도에 유효한 본인만의 Vg diagram을 가진다.
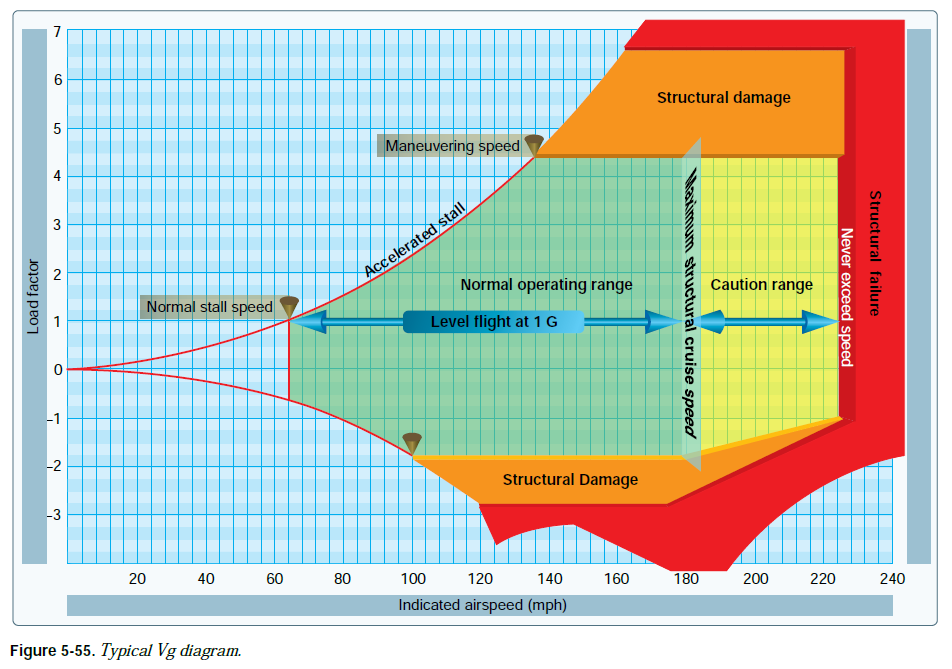
maximum positive lift capability(붉은색 곡선)는 Vg diagram에서 가장 중요한 항목이다. 그림 5-55의 항공기는 64mph(항공기의 실속 속도)에서 +1G 이하의 양력을 생산할 수 있다. 최대 하중 계수는 속도의 제곱에 따라 달라지므로 이 항공기의 maximum positive lift capability는 92mph에서 2G, 112mph에서 3G, 그리고 137mph에서 4.4G이다. 이 곡선을 초과하는 하중 계수는 공기역학적으로 사용할 수 없다. 왜냐하면 항공기가 실속에 빠지기 때문이다. 음(-)의 양력 곡선에서도 동일한 상황이 존재한다(단, 특정 음(-)의 하중 계수를 생성하는데 필요한 속도가 동일한 양(+)의 하중 계수를 생성하는데 필요한 속도보다 높다는 점 제외).
항공기가 positive limit load factor 4.4보다 높은 하중 계수로 비행하면 구조적 손상이 발생할 수 있다. 항공기가 이 구간을 운영하면 primary structure의 영구적 변형이 발생할 수 있으며 높은 비율의 피로 손상이 발생한다. 정상 운영 도중 limit load factor가 초과되는 것을 피해야 한다.
Vg diagram에는 두 가지 중요한 지점이 있다. 하나는 positive limit load factor와 maximum positive lift capability가 교차하는 지점이다. 이 지점은 공기역학적으로 limit load가 만들어질 수 있는 최소 속도이다. 이보다 높은 속도는 항공기를 손상시키기에 충분한 positive lift capability를 제공한다. 반면 이보다 낮은 속도는 과도한 비행 하중으로 인한 손상을 발생시키기에 충분한 positive lift capability를 제공하지 않는다. 이러한 속도는 보통 “maneuvering speed”라 불린다. 왜냐하면 아음속 공기역학을 고려하면 이 조건에서 발생할 수 있는 기동성이나 최소 선회 반경을 예측할 수 있기 때문이다. maneuvering speed 이하로 비행할 경우 항공기에 손상을 가하는 양(+)의 비행 하중이 생성될 수 없으므로 이는 매우 중요한 기준점이다. 항공기가 maneuvering speed 이하로 비행중이면 어떠한 기동 및 돌풍 조합도 손상을 발생시킬 수 없다.
Vg diagram에서 중요한 또 다른 지점은 negative limit load factor와 maximum negative lift capability가 교차하는 지점이다. 이보다 높은 속도는 항공기를 손상시키기에 충분한 negative lift capability를 제공한다. 반면 이보다 낮은 속도는 항공기 손상을 발생시키기에 충분한 negative lift capability를 제공하지 않는다.
limit airspeed(혹은 redline speed)는 항공기의 설계 기준점이다. 이 항공기의 경우 limit airspeed는 225mph이다. 해당 속도가 초과되면 다양한 현상으로 인해 구조적 손상이나 구조적 파괴가 발생할 수 있다.
비행 중인 항공기는 limit speed가 초과되지 않는, limit load factor가 초과되지 않는, 그리고 maximum lift capability가 초과될 수 없는 비행속도 및 하중 계수로 제한된다. 구조적 손상을 방지하기 위해, 그리고 항공기의 사용 수명을 지키기 위해 조종사는 항공기를 이 “envelope” 내에서 운영해야 한다. Vg diagram은 안전한 운항을 위해 허용하는 대기속도 및 하중 계수의 조합을 설명하므로 조종사는 이를 숙지해야 한다. structural envelope를 초과하는 기동이나 돌풍이 구조적 손상을 발생시켜 항공기의 사용 수명을 단축시킬 수 있다.
Rate of Turn
선회율은 항공기가 만드는 heading 변화율을 의미한다(초 당 도[°]로 표시됨). 선회율은 상수 1,091에 bank angle의 탄젠트를 곱한 다음 이를 특정 속도(노트)로 나누어서 구해진다. [그림 5-56] 대기속도가 증가할 때 선회율을 일정하게 유지하고자 한다면 bank angle을 증가시켜야 한다. 그렇지 않으면 선회율이 감소한다. 만약 대기속도가 일정하게 유지될 때 bank angle을 증가시키면 선회율이 증가한다. 그림 5-56 ~ 58의 공식은 bank angle과 airspeed가 선회율에 미치는 영향을 보여준다.



NOTE: 여기서 설명하는 모든 대기속도는 진대기속도(TAS)이다.
속도는 항공기의 선회율에 상당한 영향을 미친다. 만약 속도가 증가할 때 bank angle을 일정하게 유지하면 선회율이 감소한다. 따라서 속도가 증가할 때 선회율을 일정하게 유지하기 위해서는 bank angle이 증가해야 한다.
이는 실용적인 측면에서 무엇을 의미하는가? 특정 airspeed 및 bank angle이 특정 선회율을 만들어낸다면 추가적인 결론을 내릴 수 있다. 선회율을 알면 360도(원)를 이동하는데 걸리는 시간을 결정할 수 있다. 예를 들어 120노트의 airspeed와 30도 bank angle에서 선회율은 초 당 5.25도이다. 이 선회율로 선회를 한 번 완료하는데 68.6초(360/5.25 = 68.6)가 걸린다. 만약 240노트의 airspeed와 30도 bank angle을 사용하면 선회율은 대략 초 당 2.63도이다. 이 선회율로 선회를 한 번 완료하는데에는 약 137초가 걸린다. 즉, 대기속도가 증가하면 항공기가 호(arc)를 비행하는데 걸리는 시간이 증가한다.
그렇다면 이것을 이해하는 것이 왜 중요할까? 선회율을 이해하면 조종사는 특정 선회를 만드는데 필요한 거리를 결정할 수 있다. 이는 선회 반경에서 설명된다.
Radius of Turn
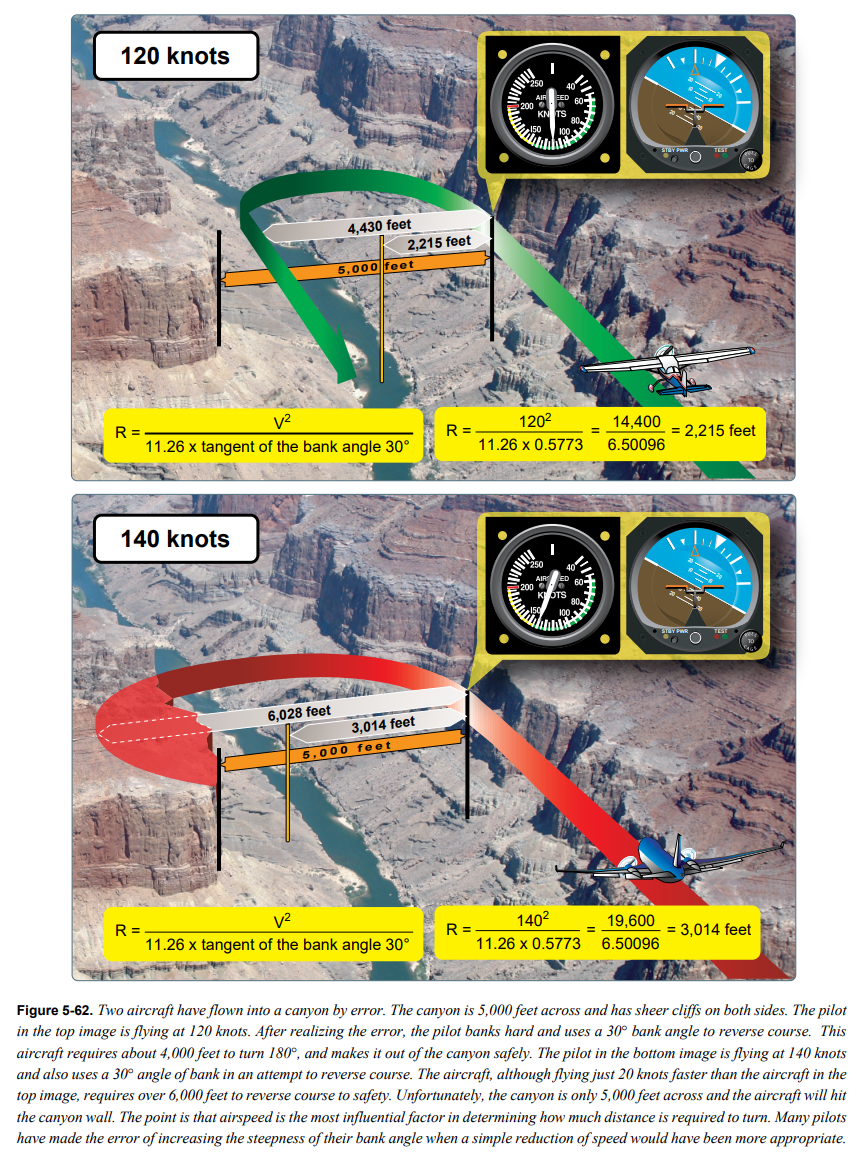
선회율은 선회 반경과 직접 연결된다. 만약 bank angle은 일정하게 유지되고 대기속도는 증가한다면 선회 반경이 증가한다. 대기속도가 높을수록 항공기는 더 긴 호를 이동한다. 120노트로 비행하는 항공기는 240노트로 비행하는 항공기보다 더 짧은 선회 반경에서 360도 원을 선회할 수 있다. 대기속도 증가를 보상하기 위해서는 bank angle을 늘려주어야 한다.
선회 반경(R)은 간단한 공식을 통해 계산될 수 있다.

그림 5-56 ~ 58의 예시를 통해 두 속도에 대한 각각의 선회 반경을 계산할 수 있다.
속도가 두 배가 되면 반지름이 네 배가 됨을 주목하라. [그림 5-59 및 60]


선회 반경을 결정하는 또 다른 방법은 초 당 피트(fps-feet per second) 속도, 파이(π=3.1415), 그리고 선회율을 사용하는 것이다. 초 당 5.25도의 선회율을 가진 항공기는 완전한 원을 만드는데 68.6초가 필요하다. 항공기의 속도(노트)에 상수 1.69를 곱하면 fps로 변환될 수 있다. 따라서 120노트(TAS)로 이동하는 항공기는 202.8fps로 움직인다. 완전한 원을 만드는데 걸리는 시간(68.6초)에 fps 속도(202.8)를 곱하면 원의 길이를 결정할 수 있다(202.8 x 68.6 = 13,912ft). 이를 파이(π)로 나누면 지름 4,428ft가 나오며 이를 2로 나누면 반지름 2,214ft가 나온다. [그림 5-61] 이는 그림 5-59의 공식을 통해 결정된 값과 거의 동일하다.

'PHAK(2023) > 5: Aerodynamics of Flight' 카테고리의 다른 글
| (10) Angle of Attack Indicators (0) | 2023.05.06 |
|---|---|
| (11) Basic Propeller Principles (0) | 2023.05.06 |
| (13) Weight and Balance (0) | 2023.05.06 |
| (14) High Speed Flight (0) | 2023.05.06 |
| (15) Chapter Summary (0) | 2023.05.06 |